Determinación del Inverso de un Punto - Estudio de Construcciones

 ¡Buenas a todxs!

Hace unas semanas en clase estuvimos intentando entender varios conceptos muy interesantes sobre geometría métrica:

"Dada una inversión definida por su centro y la potencia, hallar la circunferencia de auto-inversión, determinando el inverso de un punto usando al menos tres construcciones diferentes".

>> Teorema del Cateto:

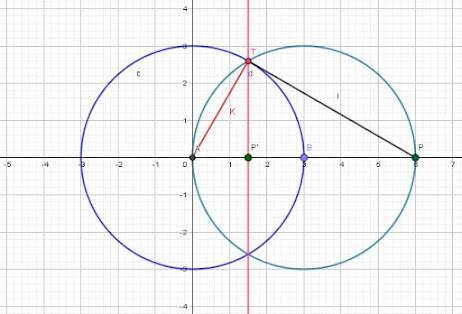
Dado el centro de inversión I , la potencia K y un punto P, hallar el inverso de este.

Lo primero que haremos será dibujar la circunferencia de auto-inversión, con centro en I y radio la potencia, K. Una vez la hallamos dibujado, deberemos realizar una circunferencia auxiliar, con centro en el punto medio entre I y P. El lugar donde esta circunferencia corte a la circunferencia de auto-inversión nos dará el punto T, desde el cual dibujaremos una recta perpendicular que corte a la recta horizontal que une I con P en el punto P'.

En esta construcción se cumplirá el teorema del cateto de la siguiente forma:

IT x IT = IP x IP' >> K x K = IP x IP'

>> Teorema del Altura:

Dado el centro de inversión I , la potencia K y un punto P, hallar el inverso de este.

Lo primero que haremos será dibujar la circunferencia de auto-inversión, con centro en I y radio la potencia, K. Una vez la hallamos dibujado, deberemos realizar una circunferencia auxiliar, con centro en el punto medio entre I y P. El lugar donde esta circunferencia corte a la circunferencia de auto-inversión nos dará el punto T, desde el cual dibujaremos una recta perpendicular que corte a la recta horizontal que une I con P en el punto P'.

En esta construcción se cumplirá el teorema de la altura de la siguiente forma:

K x K = TP x TP'

>> Teorema del Thales:

Dado el centro de inversión I , la potencia K y un punto P, hallar el inverso de este.

Lo primero que haremos será dibujar la circunferencia de auto-inversión, con centro en I y radio la potencia, K. Una vez la hallamos dibujado, deberemos realizar una circunferencia auxiliar, con centro en el punto medio entre I y P. El lugar donde esta circunferencia corte a la circunferencia de auto-inversión nos dará el punto T. Unimos I con T y P con T  para generar las rectas IT y PT que, junto con la recta base, crearán la figura de un triángulo rectángulo. Luego, no tenemos más que dibujar una recta paralela al lado PT del  triángulo, para crear un triángulo semejante a este desde O y hacia la recta K. Esta esta nueva  recta cortará a K en un punto que llamaremos Q. Así, obtendremos el punto P' al pasar la dimensión IQ a la recta base con un compás.

En esta construcción se cumplirá el teorema de Thales de la siguiente forma:

QO/QI = TP/K