Puntos Notables de los Triángulos

¡Saludos a todxs!

Los triángulos son figuras geométricas muy especiales, que contienen un montón de sorpresas geométricas... ¿Te gustaría conocerlas?

El Ortocentro (H u Oo) es el punto donde se cortan las tres alturas de un triángulo. Además, el triángulo resultante de unir las tres bases de las alturas (Ha,Hb,Hc), se denomina triángulo órtico, siendo el ortocentro el incentro de dicho triángulo. En la imagen siguiente podéis ver cómo he hallado el ortocentro y el triángulo órtico  utilizando Geogebra:

El Circuncentro (H u Oc) es el punto que encontramos cuando trazamos las mediatrices de los tres lados de un triángulo, este resulta ser el centro de la circunferencia circunscrita al triángulo:

Si trazamos las bisectrices de los tres ángulos internos de un triángulo, estas se cortarán en un mismo punto, que se denomina Incentro(Oi), y que resulta ser el centro de la circunferencia inscrita al triángulo:

Hoy no vamos a profundizar sobre esto, pero os avanzo que existen unos lugares geométricos bastante interesantes una vez que empezamos a experimentar con los triángulos:

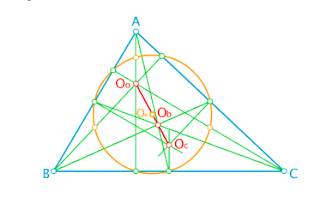
En todo triángulo, el Ortocentro(Oo), el Baricentro(Ob) y el Circuncentro(Oc) están alineados, y el segmento que definen se denomina Segmento de Euler:

Las rectas de Simpson son las rectas que unen los pies de las perpendiculares, trazadas desde un punto de la circunferencia circunscrita a los tres lados del triángulo, o sus prolongaciones:

La circunferencia de Taylor es la circunferencia que pasa por los pies de las perpendiculares trazadas desde los pies de las alturas a los lados del triángulo. Y es una circunferencia de Tucker.

Y para terminar...¡Los triángulos de Napoleón! Hoy no os contaré nada sobre ellos, ya que quiero que investiguéis un poco. Os dejo la imagen tan curiosa de estos triángulos para tentaros a investigar :)

Un abrazo para todxs y...¡Hasta la próxima!