Problema Fundamental de Tangencias

 

El problema fundamental de tangencias, consiste en determinar la/s circunferencia/s que pasan por dos puntos (C y D) y son tangentes a una recta (r). 

Existen dos maneras de resolverlo: la primera es hacerlo como si fuese una receta (un poco de esto, un poco de aquello y...¡Problema resuelto!),  la segunda es entendiendo por qué se hace lo que se hace, y esta última es que voy a tratar de desarrollar en este post. 

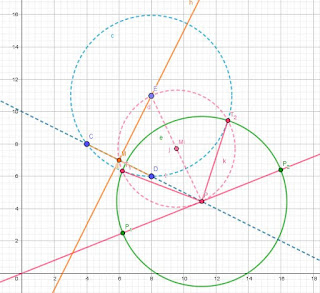
Lo primero de todo sería dibujar los puntos "C" y "D" y la recta "r", analizando las posibles soluciones. Éstas pasarán por los puntos "C" y "D", y serán tangentes a "r". Al final lo que necesitamos  son los centros de las circunferencias solución, es decir, puntos. Como sabemos, un punto está definido por dos datos, que  pueden ser sus coordenadas x e y u otros dos cualesquiera que nos permitan encontrarlos.  Lo que ya sabemos es que los centros de las circunferencias solución se encontrarán en la mediatriz del segmento CD, ya que siempre se cumple que la mediatriz de cualquier cuerda de una circunferencia pasa por el origen.  Así pues, ya tenemos un dato para resolver el ejercicio.

Otra cosa que también sabemos es que los radios de las circunferencias que unen los puntos de tangencia con cada uno de sus centros son perpendiculares a "r". Lo que no sabemos es por qué puntos  trazar esa perpendicular. Este es el segundo dato que nos falta, y que podemos hallar. Este es el momento en el que debemos recurrir al concepto de potencia, ya  que este va a suponer la herramienta principal para resolver cualquier tipo de tangencia. ¿Por qué es tan útil la potencia? Pues porque la potencia desde un punto es constante independientemente de los puntos de la circunferencia que consideremos, lo que nos va a permitir establecer una relación entre todas las circunferencias que pasan por dos puntos.

Las circunferencias solución van a pasar por tres puntos: por "C", por "D" y por los puntos de tangencia con la recta "r" (P1 y P2), o sea que lo que tenemos que hallar son estos dos puntos desde los que trazar los radios perpendiculares. Además, sabemos que la potencia desde un punto "P" según la dirección de la recta que pasa por "C" y por "D" es la misma que la potencia de las rectas desde "P" a los puntos de tangencia (P1 y P2), lo que hay que hallar es el valor de esta potencia. Llegados a este punto os preguntaréis dónde está "P".  Pues bien, para que se cumpla la condición anterior "P" tiene que estar en la intersección de la recta que pasa por "C" y "D" con la recta "r".

Ya tengo "P" pero, ¿cuál es el valor de la potencia?. Como la potencia desde un punto "P" es constante a cualquier circunferencia que pasa por "C" y "D", ¿no me valdría cualquier circunferencia que pase por estos puntos para calcular la potencia...? ¡Pues sí!. 

Hacemos por tanto una circunferencia auxiliar cualquiera, y hallamos el segmento de potencia (el segmento tangente desde "P" a la circunferencia auxiliar).

Realizamos por tanto el arco capaz de 90 grados del segmento formado por el punto "P" y el centro de la circunferencia auxiliar, y su intersección con la circunferencia auxiliar nos dará los puntos de tangencia y por tanto el segmento de la potencia que estamos buscando.

Conocida la longitud de este segmento solo tengo que trasladarlo sobre la recta "r" desde "P" (recuerda hemos dicho que la potencia es la misma, y por tanto la longitud de este segmento también) para localizar los puntos "P1" y "P2" de tangencia con las circunferencias solución.

Si ahora trazo las perpendiculares a "r" por los puntos de tangencia (P1 y P2), ¡las intersecciones de estas perpendiculares con la mediatriz del segmento CD, serán los centros de las circunferencias solución!

Para resolver el ejercicio también podrían utilizarse otros métodos, como empleando el teorema del cateto o el teorema de la altura.